Lucas (1990) “Why Doesn’t Capital Flow from Rich to Poor Countries?”#
Summary and analytical notes on the paper:
Lucas, Robert E. (1990) “Why Doesn’t Capital Flow from Rich to Poor Countries?” American Economic Review: 92-96.
Neoclassical predictions:#
the convergence of factor prices and incomes per-capita over time (Factor Price Equalization Theorem)
via substitute mechanisms: factor movement, trade in products, and/or capital accumulation (e.g. Solow).
rests on assumptions about technology and market competition
in particular: diminishing returns to the accumulated factor capital (i.e. \(F_{KK} < 0\) ).
Simplest model#
Assume two countries with same aggregate production function, where \(X\) is capital stock and \(L\) is labor force:
in intensive or per-capita form: $\(y = A x^\beta\)$
where $\(y = \frac{Y}{L} \text{ and } x = \frac{X}{L}\)$
Marginal Product of Capital (MPK) is:
Write MPK as a function of income per capita:
or
Steps:
so $\(x = \left ({\frac{y}{A}} \right)^\frac{1}{\beta} \)$
substitute this into \(r = A \beta x^{\beta -1}\)
The puzzle#
Let capital share \(\beta =0.4\) (average of USA and India)
Assume first that \(A\) is the same in both countries
In 1988 income per capita in USA was 15 times higher than USA:
this implies MPK in India would have to be:
times higher in India! Implausibly large.
What differences in capital per worker account for this large a gap?
As \(x = \left ({\frac{y}{A}} \right)^\frac{1}{\beta} \) and \(\frac{y_{US}}{y_{IN}} = 15\), US workers would have to have this
multiple of the amount of capital per worker compared to India:
So if in India the capital-labor ratio is 1 in the USA it must be 871.4 !
With such huge differences in returns, capital would surely RUSH from USA to India quickly lower the gap in returns and incomes.
Evidently it does not. So what’s wrong with the model? Lucas walks through 4 alternate hyptotheses.
Some plots#
Show code cell source
import numpy as np
import matplotlib.pylab as plt
from scipy.optimize import fsolve, brentq, minimize
Show code cell source
A = 1
rho = 0.05
beta = 0.4
y_US = 15
y_IN = 1
def f(x):
return x**beta
def mpx(x):
return beta*x**(beta-1)
def r(y, A):
return beta * (A**(1-beta)) * y**((beta-1)/beta)
def kap(y, A):
return (y/A)**(1/beta)
def xoptimum(rho, beta):
xC = (rho/beta)**(1/(beta-1))
xM = (rho/beta**2)**(1/(beta-1))
return xC, xM
Show code cell source
def lucasplot():
y = np.linspace(0.1,20,100)
plt.figure(figsize=(12, 6))
plt.subplot(2,1,1)
plt.plot(y,kap(y, A))
plt.ylabel("$k$ -- capital per worker")
plt.ylim(0,kap(y_US +1, A))
plt.axvline(y_IN,color='k',ls='dashed')
plt.axvline(y_US,color='k',ls='dashed')
plt.title("capital per worker")
plt.subplot(2,1,2)
plt.plot(y,r(y,A))
plt.xlabel("$y$ -- output per worker")
plt.ylabel("$4$ -- marginal product capital")
plt.title("return to capital")
plt.ylim(0,r(y_IN,A))
plt.axvline(y_IN,color='k',ls='dashed')
plt.axvline(y_US,color='k',ls='dashed')
plt.annotate('India', xy=(y_IN, r(y_IN,A)), xytext=(y_IN +2, r(y_IN,A)*0.75),
arrowprops=dict(facecolor='black', shrink=0.05),)
plt.annotate('USA', xy=(y_US, r(y_US,A)), xytext=(y_US +2, r(y_US,A)+0.1),
arrowprops=dict(facecolor='black', shrink=0.05),);
Show code cell source
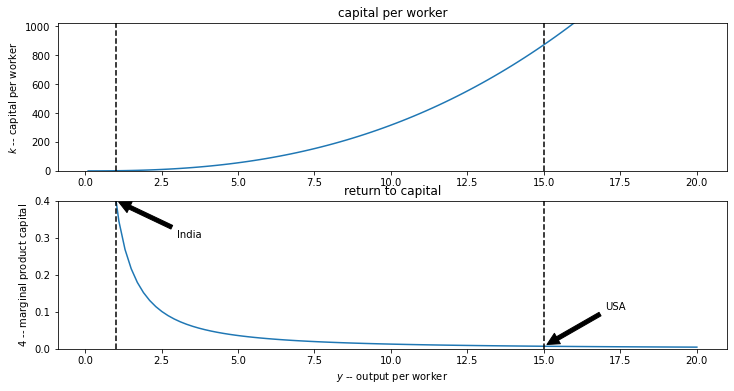
print('Return to capital in India relative to USA : {:5.1f}'.format(r(y_IN, A)/r(y_US, A)))
Return to capital in India relative to USA : 58.1
The ratio of capital stock per worker in the USA compared to India that is implied by this difference in incomes per capita is even more unbelievable:
Show code cell source
print('Capital per worker in USA relative to India : {:5.1f}'.format(kap(y_US, A)/kap(y_IN, A)))
Capital per worker in USA relative to India : 871.4
lucasplot()
The four hypotheses:#
Differences in Human Capital (effective labor)
External Benefits of Human Capital (increasing returns)
Capital Market Imperfections I (political risk)
Capital Market Imperfections II (monopoly distortions)
Hypothesis 1: Human Capital differences#
Human capital per worker differs substantially between USA and India. Let’s adapt the framework to take this into account.
Redefine \(y\) and \(x\) to be output and capital per effective worker (replace every \(L\) by \(E \cdot L\)).
or $\(y=Ax^\beta \cdot E ^{-\beta}\)$
Lucas’ cites evidence from Anne Krueger that leads him to suggest a value of \(E =5\), which is to say that for the same technology and capital a US worker produces five times as much as his/her Indian counterpart.
To see this first note that if we take the ratio of US to Indian income per effective worker we get:
With this we can easily calculate the implied difference in marginal products of capital:
So this lowers the factor of proportionality from 58 to 5. As Lucas puts it: “This is a substantial revision but it leaves the original paradox very much alive: a factor of five differnce in rates of return is tstill large enough to lead one to expect capital flows much larger than anything we observe (p. 93).”
Hypothesis 2: Human Capital Spillovers#
We’ve assumed thus far that the total factor productivity parameter \(A\) is the same across countries. This is unlikely. An easy way to resolve the paradox is to simply solve for the level of A_{US}/A_{IN} that makes he gap dissappear.
In this section Luca isn’t quite doing that but he is in effect letting the values of A differ between the two countries. He motivates this with a stripped down version of his own Lucas (1988) paper on external economies, a model where human capital plays a role and where there is a positive external effect in human-capital accumulation in that he assumes that the marginal product of one’s human capital is augmented by the average level of human capital in the economy. In this paper he doesn’t work out this model in full but uses the story to rewrite the production function as:
and he then gives us some ‘guestimates’ as to the differences in human capital per worker in each country.
As it turns out this is in effect equivalent to sticking to the original model and just assuming that $\(\frac{A_{US}}{A_{IN}} = 5\)$
A country with a higher level of \(A\) will have everywhere higher return on capital. After a little math the adjusted ratio now becomes
This would seem to almost resolve the paradox but Lucas in fact dismisses it as not entirely realistic. It assumes for example that knowledge spillovers across borders are zero.
Hypothesis 3: Capital Market Imperfections#
Capital flows would be in the form of debt (or share) contracts with loans/investment flowing from rich to poor countries in an initial phase followed by a long repayment phase. Lucas’ discussion on this topic is limited to observing that one could imagine problems of sovereign default, with debtor country defaulting on repayment obligations, and how the anticipation of this problem might reduce capital flows. He points out that contracts were more enforceable in the colonial era, as the poor countries were not sovereign so contracts were enforceable throughtout empires yet the same capital flow puzzles persisted.
Hypothesis 4: Market power distortions#
Lucas last and most intriguing hypothesis, which he partly attributes to Adam Smith, is that local elites (or ‘an imperial power’) might be colluding to limit the entry of capital into poor countries in order to drive up capital rents and drive down real wages in such a way that increase elite earnings from capital and firm profits.
While it might seem far-fetched to believe a story like this in modern times (less so in East India Company times) there is a considerable literature arguing that local elites lobbty governments for capital controls to protect the rents of local elites. Rajan and Zingales’ (2013) book Saving Capitalism from the Capitalists is full of examples of manipulated local financial markets.
The elite is assumed to have access to international capital markets where they can borrow capital at the rate \(\rho \)
If the elite ran the country as a monopoly they would choose the capital-labor ratio (by varying how much capital enters the country) to maximize profits per capita:
One way to interpret this formulation is that there is a large monopolist that has access to capital at the world interest rate \(r\) but then rents it out at the marked up rate \(f'(x)\) to a ‘fringe’ of smaller competitive firms who produce the common output. The competitive fringe hires factors until the marginal value product equals the market factor price. By restricting capital into the economy the monopolists drive up the domestic rental price of capital. With less capital per worker labor is less productive and this drives down the mearket equilibrium real wage (\(f(x)-xf'(x)\)).
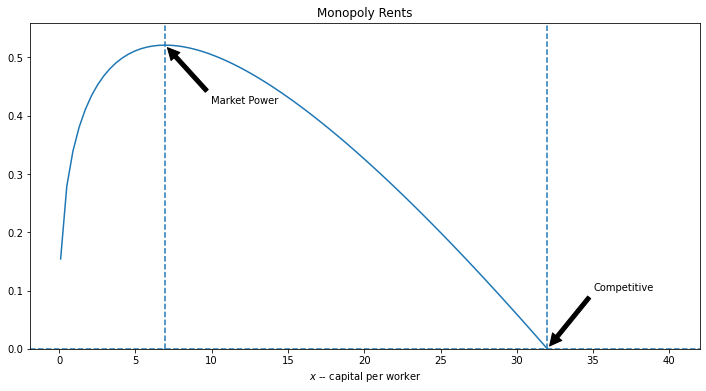
Let’s plot that profits per capita function (which is also the value of economic rents from capital per capita \((f'(x) - \rho)\cdot x\):
Show code cell source
x = np.linspace(0.1,40,100)
def profit(x, rho):
return f(x) -(f(x) -mpx(x)*x) - rho*x
def monopolyplot(rho):
prf = profit(x, rho)
xC, xM = xoptimum(rho, beta)
fig, ax = plt.subplots(1, 1, figsize=(12, 6))
plt.plot(x, prf)
plt.ylim(bottom=0.)
plt.title('Monopoly Rents')
plt.axvline(xC,ls='dashed')
plt.axvline(xM,ls='dashed')
plt.axhline(0,ls='dashed')
plt.xlabel("$x$ -- capital per worker")
plt.annotate('Competitive', xy=(xC, 0), xytext=(xC+3, 0.1),
arrowprops=dict(facecolor='black', shrink=0.05),)
plt.annotate('Market Power', xy=(xM, profit(xM,rho)), xytext=(xM+3, profit(xM,rho)-0.1),
arrowprops=dict(facecolor='black', shrink=0.05),)
plt.show()
monopolyplot(rho=0.05)
In an open competitive economy these economic rents would have been driven to zero and the capital-labor ratio \(x\) would be simply set from
where \(\rho\) is the world market price of capital. This implies we can find the competitive equilibrium capital labor ratio as a function of \(\rho\):
Suppose we set the world rate or return to capital to \(\rho=0.05\). Then equlibrium capital per worker in the competitive economy would be:
Show code cell source
rho, beta = 0.05, 0.4
xC, _ = xoptimum(rho, beta)
print('%.1f' % xC)
32.0
On the other hand, the monopolist sets x to satisty a first order condition which sets marginal revenue equal to marginal cost:
Note that $\(f''(x) =(\beta -1) \frac{f'(x)}{x}<0\)$
The monopolist is aware of the downward sloping domestic demand for capital and searches for a profit maximizing price-quantity combination along that curve.
The monopoly FOC simplifies to:
Given our assumed value of beta, this means a monopolist might maintain the rate of return on capital \(1/ \beta\) times higher than the international market rate \(\rho\), and resists capital inflows that might push this rate down.
Solving for \(x\) in this monopolized market gives:
Which is obviously lower than the efficient competitive level.
Show code cell source
_ , xM = xoptimum(rho, beta)
print('Capital per worker in the market-power distorted equilibrium: {:2.1f}'.format(xM))
print(' {:.0%} of the competitive level'.format(xM/xC))
Capital per worker in the market-power distorted equilibrium: 6.9
22% of the competitive level
This implies that Indian income per capita will be only
Show code cell source
print(f'{100*f(xM)/f(xC):5.0f} percent')
54 percent
as high as in a competitive market without barriers to capital inflows.
This is an inefficient outcome but the elites who capture the profits/rents do well. They earn
print(f'profits = {profit(xM, rho):5.2f} or {profit(xM,rho)/f(xM):.0%} of total output')
profits = 0.52 or 24% of total output
Extensions#
Lucas does not cite their work but models of this sort were explored by trade economists in the 1980s (e.g. Feenstra (1980). In a later notebook we’ll see Conning (2006) exploration of similar factor market power distortions in a model with heterogenous agents to make predictions about the size distribution of firms within each sector.
Solving for maxima and roots numerically#
This model was easy to solve analytically, but let’s also solve it numerically just to illustrate the ease of using numerical root solving and minimization techniques in python.
Let’s setup first order condition functions to find the x that sets them to zero.
For the competitive case: \(f'(x) = \rho \) For the monopoly case: \(f'(x) - x f''(x) = \rho\)
def cfoc(x):
return mpx(x) - rho
def mfoc(x):
return mpx(x) - rho + (beta-1)*mpx(x)
Solve the competitive FOC for \(x\), by finding the root of \(f'(x)-\rho = 0\):
xC = fsolve(cfoc, 20)[0]
xC
32.0
Same as the analytical solution of course.
Now let’s find the \(x\) that maximizes monopoly profits (we need to provide a guess value):
xM = fsolve(mfoc, 5)[0]
xM
6.948909098482633
We could have instead directly maximized profits (minimized negative profits) with an optimization routine:
def negprofit(x):
return - profit(x, rho)
res = minimize(negprofit, 5, method='Nelder-Mead')
res.x[0]
6.94891357421875