Farm Household Models#
Economics textbooks typically present the decisions of firms in one set of chapters and the consumption decisions of households in separate chapters. In this artificial but useful dichotomy the firm organizes production and hires factors of production to maximize profits while households own the factors of production (and ownership shares in firms). Households earn incomes from supplying these factors to firms and use that income to purchase products from the firms. We treat these decisions as ‘separable’.
Many households are however simultaneously producers and consumers. They may operate small farms, garden plots, stores or other types of businesses, and at the same time sell or hire labor in the labor market. In fact a large literature suggests that one defining characteristic of developing countries labor markets is the large fraction of its labor force that are self-employed ‘own account’ workers, many of whom run small businesses alongside wage labor jobs (Gollin, 2008).
Here we offer stylized representations of the so called ‘farm household model’ or ‘agricultural household model’ (Singh, Squire, Strauss, 1986). In these models the household acts both as a consumption unit, maximizing utility over consumption and ‘leisure’ choices as well as a production unit, deciding how much labor and other factors to allocate to the the household farm or business, and how much to the market.
A key question in this literature is whether the household’s production decisions (such as its choice of labor and other inputs and the scale of production) are separable or not from its preferences and endowments (e.g. consumer preferences, household demographic composition and ownership of land and other resources). For example, will a rural farm household with more working age adults run a larger farm compared to a neighboring household that is otherwise similar and has access to the same technology but has fewer working-age adults? Standard ‘separable’ theory would say that with well functioning factor markets the optimal size of the farm should be independent of the farm owners’ preferences and factor ownership – the farm operators should maximize profits guided only by market product and factor prices. On the other hand, if the households decisions are non-separable, perhaps because of labor of land factor market imperfections, then the answer might instead be yes: the larger household might run a larger or more labor-intensive farm.
When households are embedded in well functioning competitive markets the household’s decisions should become separable. In other words we can the:
Household as a profit-maximizing firm: acting as a profit-maximizing firm the household first optimally chooses labor and other input allocations to obtain maximized profits from the farm.
and, separately, we can analyze the:
Household as a consumption unit: the household makes optimal choices over consumption and leisure subject to its income budget which includes income from selling its labor endowment and maximized profits from the household as a firm.
In the simple example above, of two otherwise identical households with access to the same technology and markets but one having a larger labor endowment, the separable farm household model would predict that both households would run farms of identical size and use wage labor markets to equalize land-labor ratios, and hence marginal products of labor, across farms. The larger household would be a larger net seller of labor on the market compared to the smaller household.
If the separation property does not hold, the common approach of many studies of estimating consumer demand independently of estimates of output supply would no longer valid.
Another way to state the separation hypothesis is that if households have full access to markets then marginal production decisions should not depend on their owners’ preferences in consumption or their ownership of tradable factors. When markets are complete then production decisions will be separable, the price mechanism will equalize the marginal products of factors across uses, and the initial distribution of tradable factors should not matter for allocative efficiency – the first and second welfare theorems will hold.
Much of modern micro-development, since at least the mid 1960s has however been concerned with how transactions costs, asymmetric information, or costly enforcement and conflict can lead to market frictions and imperfections that make production decisions non-separable. Then the initial distribution of property rights (over land and other tradable factors) may in fact matter for determining the patterns of production organization and its efficiency in general equilibrium.
One good early general equilibrium modeling of an economy where the the initial distribution of assets affects the structure and efficiency of production organization is Eswaran and Kotwal’s (1986) paper on “Access to Capital and Agrarian production organization.” This explores how the combination of transaction costs in labor hiring and in access to capital can lead to a theory of endogenous class structure or occupational choice and how this class structure can change dramatically depending on the initial distribution of property rights.
The Chayanovian Household#
We’ll start with a non-separable model, inspired by the work of the Russian agronomist Alexander Chayanov whose early 20th century ideas on “the peasant economy” became widely influential in anthropology, economics, and other fields. Chayanov played a role in early Soviet agrarian reforms but his focus on the importance of the household economy led him to be (presciently) skeptical of the appropriateness and efficiency of large-scale Soviet farms. He was arrested, sent to a labor camp, and later executed.
The following model is not anywhere as rich as Chayanov’s description of the peasant household economy but a stripped down version closer in spirit to Amartya Sen’s (1966) adaptation.
Farm household \(i\) has land and labor endowments \((\bar T_i, \bar L_i )\). We can assume that it can buy and sell the agricultural product at a market price \(p\) but in practice we will model the household as self-sufficient and cut-off from land and labor factor markets. The household (which we treat as a single decision-making unit for now) allocates labor maximizes utility over consumption and leisure
It’s useful to think of the utility function \(U(c_i,l_i;A)\) as depending on ‘preference shifters’ \(A\) which might include such things as the household’s demographic composition or things that affect it’s preference for leisure over consumption).
The household maximizes this utility subject to the constraints that consumption \(c_i\) not exceed output and that the sum of hours in production \(L_i\) plus hours in leisure \(l_i\) not exceed the household’s labor endowment \(\bar L_i\)
Substituting the constraints into the objective allows one to redefine the problem as one of choosing the right allocation of labor to production:
From the first order necessary conditions we obtain
which states that the farm household should allocated labor to farm production up to the point where the marginal utility benefit of additional consumption \(U_c \cdot F_L\) equals the opportunity cost of leisure.
The household sets the marginal product of labor (or shadow price of labor) equal to the marginal rate of substitution between leisure and consumption \(F_L = U_l/U_c\). Since the latter is clearly affected by ‘preference shifters’ \(A\) and also by the household’s land endowment, the shadow price of labor will differ across households that are otherwise similar (say in terms of their access to production technology and farming skill). For example households with more dependents might have a different tradeoff between consumption and leisure.
It will be useful to draw things in leisure-consumption space. Leisure is measured on the horizontal from left to right which then means that labor \(L\) allocated to production can be measured from right to left with an origin starting at the endowment point \(\bar L_i\)
To fix ideas let’s assume farm household \(i\) has Cobb-Douglas preferences over consumption and leisure: $\(U(c,l) = c^\beta l^{1-\beta}\)$
and its production technology is a simple constant returns to scale Cobb-Douglas production function of the form:
The marginal product of labor \(F_L\) which the literature frequently refers to as the shadow price of labor will be given by:
The first order necessary condition can therefore be solved for and for these Cobb-Douglas forms we get a rather simple and tidy solution to the optimal choice of leisure
where \(a=\frac{1-\beta}{\beta \cdot (1-\alpha)}\)
Graphical analysis#
from farmhh import *
ALPHA = 0.5
BETA = 0.7
TBAR = 100
LBAR = 100
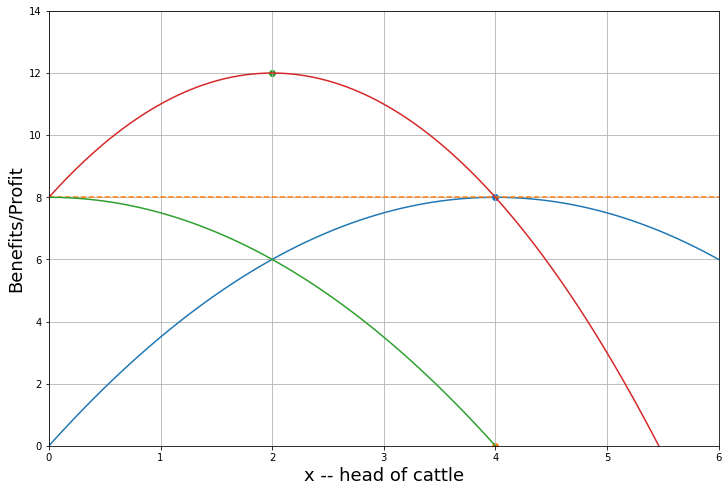
chayanov(TBAR,LBAR,0.5,0.5)
Leisure, Consumption, Utility =(66.67,57.74,62.04)
shadow price labor: 0.87
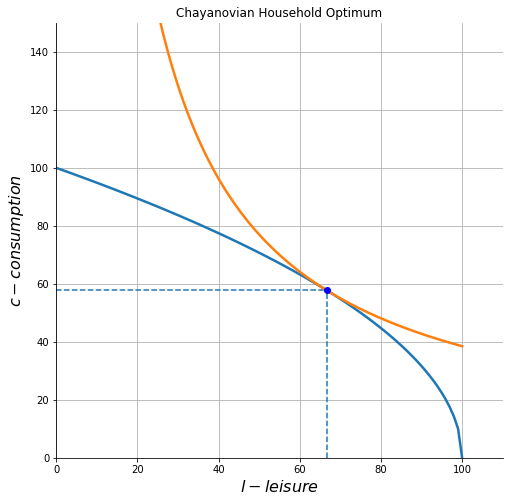
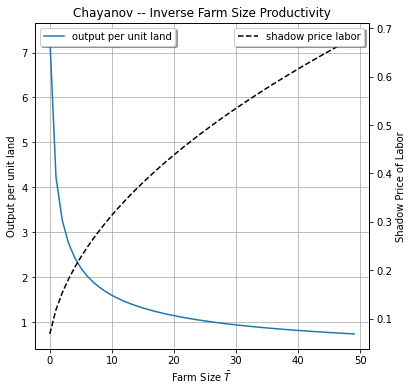
Inverse farm size productivity relationship#
For this non-separable household, if there is no market for land or labor, each household will farm as much land as it owns. We find thecommonly found inverse relationship between farm size and productivity: output per hectare is higher on smaller farms (here for the obvious reason that there will be more labor per unit of land). Households with larger farms enjoy higher marginal products of labor – a higher shadow price of labor, but lower marginal product of land.
These two relationships can be seen below on this two-axis plot.
Show code cell source
Tb = np.linspace(1,LBAR)
le, q, _ = HH(Tb,LBAR)
fig, ax1 = plt.subplots(figsize=(6,6))
ax1.plot(q/Tb,label='output per unit land')
ax1.set_title("Chayanov -- Inverse Farm Size Productivity")
ax1.set_xlabel('Farm Size '+r'$\bar T$')
ax1.set_ylabel('Output per unit land')
ax1.grid()
ax2 = ax1.twinx()
ax2.plot(FL(Tb,LBAR-le),'k--',label='shadow price labor')
ax2.set_ylabel('Shadow Price of Labor')
legend = ax1.legend(loc='upper left', shadow=True)
legend = ax2.legend(loc='upper right', shadow=True)
plt.show()
If you are running this notebook in interactive mode you can play with the sliders:
interact(chayanov,Tbar=(50,200,1),Lbar=(24,100,1),alpha=(0.1,0.9,0.1),beta=(0.1,0.9,0.1));
The Separable Farm Household#
Consider next the case of the household that can buy or sell output on the product and hire in or hire out on land and labor markets.
The household can buy and sell the consumption good at market price \(p\) and buy or sell labor at market wage \(w\). Hired labor and own household labor are assumed to be perfect substitutes. To keep the analysis a little bit simpler and fit everything on a single graph we’ll assume that the market for land leases remains closed. However it is easy to show that for a linear homogenous production function this will not matter for allocative efficiency – it will be enough to have a working competitive labor market for the marginal product of land and labor to equalize across farms.
When the farm household is a price-taker on all markets like this, farm production decisions become ‘separable’ from farm consumption decisions. The farm household can make its optimal decisions as a profit-maximizing farm and then separately choose between consumption and leisure subject to an income constraint.
The household’s problem can be expressed as:
s.t. $\(p \cdot c \leq pF(\bar T_i,L^*) + w \cdot (\bar L_i - l)\)$
This last constraint states that what the household spends on consumption (\(p\cdot c\)) cannot exceed the value of farm sales at a profit maximizing optimum plus wage income from labor sold to the market. This constraint can be rewritten as:
where \(\Pi (T_i,w,p) = p \cdot F(T_i,L^*_i) - w \cdot L^*_i\) is the maximized value of farm profits and \(L^*_i\) is the optimal quantity of labor that achieves that maximum. This states that what the household spends on consumption and leisure cannot exceed total income. The household ‘purchases’ leisure at the market wage rate since the opportunity cost of each hour of leisure is given by the market wage that could have been earned with tat hour.
The farm household can be thought of as maximizing profits by choosing an optimal labor input into the farm \(L^*_i\) which can be satisfied with own and/or hired labor.
The efficient competitive farm#
As a production enterprise, the farm acts to maximize farm profits \(pF(\bar T_i,L_i) - w \cdot L_i \). The first-order necessary condition for an interior optimum is:
The separation property is immediately apparent from this first order condition, as this equation alone is enough to determine the farm’s optimum labor demand which depends only on the production technology and the market wage, and not at all on household preferences. While the quantity of labor demanded here does depend on the households’ ownership of land, since all farms face the same market wage rate \(w\) the marginal value product of labor will be equalized across farms and equal to the common wage.
For the Cobb-Douglas production function, optimal labor demand can be solved to be:
Substituting this into the profit function, we can find an expression for farm profits \(\Pi (T_i, w, p)\) as a function of the market product price and wage and the farm’s land holding. If we had allowed for hiring on both land and labor markets we would have found zero profits with this linear homogenous technology so in this context where there is no working land market, profits are just like a competitively determined rent to non-traded land (equal in value to what the same household would have earned on its land endowment had the land market been open).
Note how the optimal allocation of labor to the farm is independent of the size of the household \(\bar L_i\) and household preferences. If we had allowed for a competitive land market the labor allocation would also have been independent of the household’s land holding.
Household demand for consumption and leisure is given very simply by the constant expenditure formula characteristic of Cobb-Douglas utility:
where household income \(I\) is given by the sum of farm profits and the market value of the factor endowment:
In what follows we shall normalize the product price \(p\) to unity. This is without loss of generality as all that matters for real allocations is the relative price of labor (or leisure) relative to output, or the real wage \(\frac{w}{p}\). So in all the expressions that follow when we see \(w\) it should be thought of as \(\frac{w}{p}\)
Let’s assume the market real wage starts at unity:
W = 1
Here is an example of a household that works and their own farm and sells labor to the market:
farmHHplot(W=1, TBAR=100)
25.0 125.0
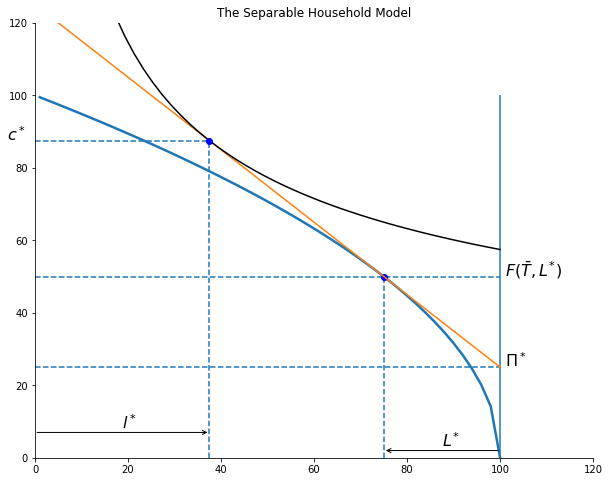
Here below is the same household when facing a much lower wage (55% of the wage in the diagram above). At this lower wage the farm will want to hire more labor to expand output on the farm and also cut back on labor sold to the market (expand leisure). This household becomes a net hirer of workers.
Show code cell source
farmHHplot(W=0.55, TBAR=100)
45.45454545454545 100.45454545454547
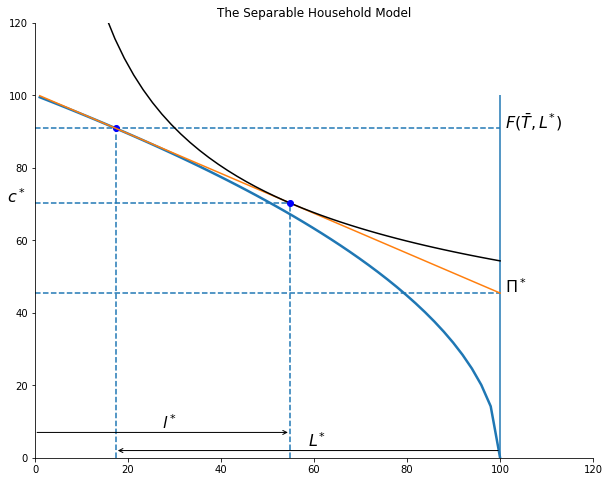
Note that the household’s endowment of land only affects the choice of leisure via income effects (higher land profits raise household income and both leisure and consumption are normal goods),
interact(farmHHplot, W=(0.5, 2, 0.1), TBAR =(50,200,1));
No Inverse farm size productivity relationship!#
Since every farm takes the market wage as given the marginal product of labor will be equalized across farms. The shadow price of labor will equal the market wage on all farms, regardless of their land size. The land labor ratio and hence also the marginal product of land will also equalize across farms so output per unit land will also remain constant.
The next section describes some empirical tests of the separation hypothesis as well as models with ‘selective-separability’ where missing markets and/or transactions costs end up determining that, depending on their initial ownership of assets, some households may face different factor shadow prices depending on whether they are buyers or sellers or non-participants on factor markets.
This last example should drive home the point that when the farm household’s optimization problem is separable the farm’s optimal choice of inputs will be independent of both household characteristics and it’s endownment of tradable factors such as land and labor.
In this last example when we shut down the labor market and introduce a transaction wedge on the market for land we create a non-separable region of autarkic or non-transacting households (shaded above). A framework such as this would generate data that displays the classic inverse farm-size productivity relationship. Farms that lease in land are smaller and have higher output per hectare than larger farms that lease land out and within the autarky zone farm size is increasing in the size of the land endowment and the shadow price (and hence output per unit land) falling.