Appendix

(rough/incomplete)

(These notes need to be cleaned up and shortened, in some sections, completed)

The Planner’s objective

The socially optimal level of enclosure maximizes total output benefit to not include the total costs of enclosure \(ct_e\bar T\). Using the convenient property of the Cobb-Douglass that \(F(t_e \bar T, l_e \bar L) = F(t_e , l_e L)F(\bar T, \bar L)\) we can write the social planner’s objective as:

\[ \left[\theta\cdot F(t_e,l_e)+F(1-t_e,1-l_e)\right ]\cdot F(\bar T, \bar L)-ct_e\bar T \]

The expression in the square brackets, which we label \(Y\), measures total output in the economy for any given choice of land and labor shares \(t_e, l_e\). We then define

\[ y(t_e,l_e)=\frac{Y}{\bar T}=\left[\theta\cdot F(t_e,l_e)+F(1-t_e,1-l_e)\right ]\cdot \bar l^\alpha \]

where we have used the fact that for our Cobb-Douglass \(F(\bar T,\bar L) =\bar T^{1-\alpha} \bar L^\alpha\) we find \(\frac{F(\bar T, \bar L)}{\bar T}=\bar l^\alpha\) where \(\bar l =\frac{\bar L}{\bar T}\)​​ measures the economy-wide labor-land endowment ratio, or population density.

Labor intensity in the enclosed sector \(l_e(t_e)\)

Recall that we found expressions for how labor would be allocated to the enclosed areas, for any given enclosure rate \(t_e\). Broadly we can write:

\[ l_e(t_e)=\frac{\Lambda_\mu t_e}{1-(\Lambda_\mu-1)t_e} \]

When labor is free to move between the enclosed and unenclosed areas, as will be the case under decentralized processes and in the second-best planning benchmark the parameter will instead be:

\[ \Lambda_\mu=\left(\frac{ \alpha\theta }{1-\mu(1-\alpha)}\right)^\frac{1}{1-\alpha} \]

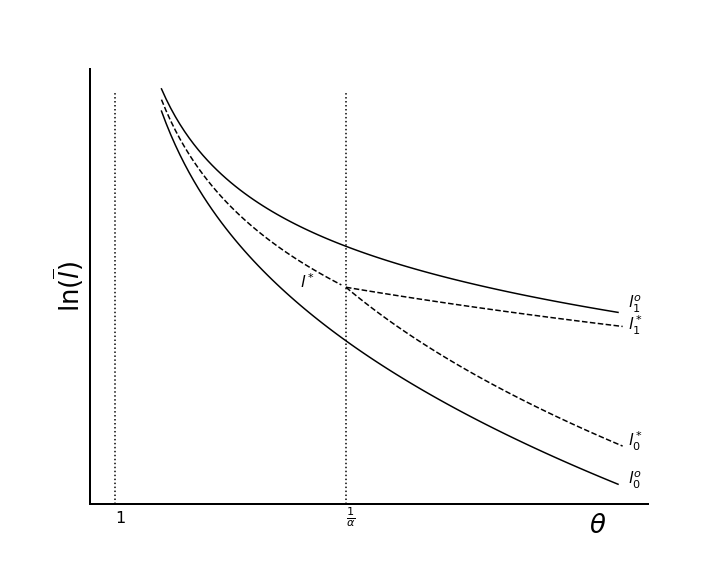
In the case of unregulated open-access we have \(\mu=0\) and we find \(\Lambda_0=(\alpha \theta)^\frac{1}{1-\alpha}\) while when access to the unenclosed areas is perfectly regulated (which is also the labor allocation chosen by a first-best social planner) we use \(\Lambda_0=\theta^\frac{1}{1-\alpha}\). The diagram below shows labor intensity \(l_e(t_e)\) as chosen by the social planner (or \(\mu=1\)), the private economy when \(\mu=0\) and in an economy with a partially regulated commons (\(\mu=0.5\))

Returning to the planner’s objective. Let’s now define

\[ z(t_e;\mu)=y(t_e,l_e(t_e)) \]

We’ve substituted \(l_e=l_e(t_e)\) using the labor intensity formula above to express total output solely in terms of the enclosure rate. When \(\mu=0\) we obtain the planner’s first-best objective \(z_1(t_e)\). When \(\mu=1\) we can the constrained social planner’s objective \(z_0(t_e)\)​.

\[ z_0(t_e) = \left[\theta F(t_e,l_e(t_e))+F(1-t_e,1-l_e(t_e))\right ]\cdot \bar l^\alpha \]

The constrained (second best) planner will enclose whenever

\[ z_0'(t_e) \ge c \]

where:

\[ z_0'(t_e) = \left[(\theta F_T^e-F_T^c)+(\theta F_L^e-F_L^c)\cdot \frac{dl_e}{dt_e} \right ]\cdot \bar l^\alpha \]

where

\[ F_T^e=\frac{\partial F(t_e, l_e)}{\partial t_e} \]

\[ F_L^e=\frac{\partial F(t_e, l_e)}{\partial l_e}\]

and

\[ -F_T^c=\frac{\partial F(1-t_e, 1-l_e)}{\partial (1-t_e)} \]

and

\[ -F_L^c=\frac{\partial F(1-t_e, 1-l_e)}{\partial (1-l_e)} \]

Further notes on notation and deriving this expression for the Cobb-Douglas case in the next section.

Notice that in a decentralized economy, private actors only enclose when

\[ \theta F_T^e \cdot \bar l^\alpha \ge c \]

So we can say that private actors ignore several “external effects.” The first is that, in this case with zero-compensation and an unregulated commons, they ignore the rents lost by those displaced by their enclosure decision (\(-F_T^c\)) . This is a “negative externality” relative to the planner’s second best which means that, all else equal, the private economy encloses too much. However there is a second effect in that the private actor ignores the positive effect \((\theta F_L^e-F_L^c)\cdot \frac{dl_e}{dt_e}\) that their enclosure has on reducing mis-allocation, as this benefit flows to others. All else equal, this effect suggests too little enclosure.

Parameters that describe the institutional and organizational environment may affect the extent to which these externalities are internalized or not because when \(\tau>0\) the encloser must pay compensation to those displaced. This means they now enclose only when \((\theta F_T^e -\tau F_T^c )\cdot \bar l^\alpha \ge c\). It is evident that when \(\tau=1\) the encloser has been forced to internalize the first external effect. But what of the second external positive spillover \((\theta F_L^e-F_L^c)\cdot \frac{dl_e}{dt_e}\)? Recall that when access to the unenclosed areas is regulated by parameter \(\mu\) (we can think of it as an access fee, or as the fraction of land possessed that a laborer can hold onto if they leave the unenclosed areas. Recall how parameter \(\mu\) affects equilibrium in the labor market:

\[ \theta F_L^e-F_L^c=(1-\mu)F_T^c\frac{T_c}{L_c} \]

It should be clear that when \(\mu=1\) the second external effect \((\theta F_L^e-F_L^c)\cdot \frac{dl_e}{dt_e}\) goes to zero. As discussed in the main text, however, both \(\mu\) and \(\tau\) need to be adjusted to arrive at a social optimum when \(\tau=\mu=1\). Adjusting one variable and not the other can make things worse.

Derivations

It’s useful to note that

\[ 1-l_e(t_e)= \frac{1-t_e}{1+(\Lambda-1)t_e} \]

Note also that after some simplification:

\[ \frac{dl_e(t_e)}{dt_e}= \frac{\Lambda}{(1+(\Lambda-1)t_e)^2} \]

and

\[ \frac{d(1-l_e(t_e))}{dt_e}=- \frac{dl_e(t_e)}{dt_e} \]

and obviously \(\frac{d(1-t_e)}{dt_e}=-1\)

So, just to be clear about notation, we got the earlier expression \(z'(t_e)\) from the chain rule:

\[\begin{split} z'(t_e) = \theta \frac{\partial F(t_e,l_e)}{\partial t_e} + \frac{\partial F(1-t_e, 1-l_e)}{\partial (1-t_e)} \frac{d(1-t_e)}{dt_e} +\theta \frac{\partial F(t_e,l_e)}{\partial l_e}\frac{dl_e(t_e)}{dt_e} + \frac{\partial F(1-t_e, 1-l_e)}{\partial (1-l_e)}\left (-\frac{dl_e(t_e)}{dt_e} \right ) \\ =(\theta F_T^e - F_T^c) + (\theta F_L^e - F_L^c) \cdot \frac{dl_e(t_e)}{dt_e} \end{split}\]

We can now find expressions for the components of \(z'(t_e)\). Note how we substitute in for \(l_e(t_e)\):

\[ \theta F_T^e=\theta \frac{\partial F(t_e,l_e)}{\partial T} =\theta (1-\alpha) t_e^{-\alpha} \left ( \frac{\Lambda t_e}{1+(\Lambda-1)t_e} \right)^\alpha =\theta (1-\alpha) \left ( \frac{\Lambda}{1+(\Lambda-1)t_e} \right )^\alpha \]

And by similar derivation (substituting in from above for \((1-l_e(t_e))\):

\[ -F_T^c= \frac{\partial F(1-t_e,1-l_e)}{\partial T} =- (1-\alpha) (1-t_e)^{-\alpha} \left ( \frac{1-t_e}{1+(\Lambda-1)t_e} \right)^\alpha =-(1-\alpha) \left ( \frac{1}{1+(\Lambda-1)t_e} \right )^\alpha \]

As described in the paper, after quite a bit of manipulation, the \(z(t_e)\) function can be simplified to

\[ z(t_e) = \bar l^{\alpha} \cdot \left[ 1+\left(\Lambda_o-1\right)t_e\right]^{1-\alpha} \]

Which leads to:

\[ z'(t_e)=(1-\alpha)(\Lambda_0-1) \cdot \bar l^\alpha\cdot \frac{1}{[1+(\Lambda_o-1)t_e]^\alpha} \]

And the condition for enclosure is:

\[ z^\prime(t_e)>c \]

which is directly comparable to the private decision:

\[ r(t_e)>c \]

Enclosure decisions are guided by:

• \(z\) concave as long as \(\theta>1\)

• \(z'(0)<c\) so zero enclosure \(t_e=0\)

• \(z'(1)>c\) so full enclosure \(t_e=1\)

• \(z'(0)>c\) and \(z'(1)<c\) so interior optimum \(t_e\)

All the loci expressions are derived same way (e.g. from \(z'(0)<c\)​)

\(z'(t_e)\)​ Components

Using the Cobb-Douglas we can get closed form solutions:

\[ \theta F_T^e=\theta (1-\alpha)\frac{\Lambda^\alpha}{(1+(\Lambda-1)t_e)^\alpha} \]

\[ F_T^c= (1-\alpha)\frac{1}{(1+(\Lambda-1)t_e)^\alpha} \]

which implies

\[ (\theta F_T^e-F_T^c)= (1-\alpha)\frac{(\theta \Lambda-1)}{(1+(\Lambda-1)t_e)^\alpha} \]

#TODO: complete other terms and show plot… Note that these are terms for the second-best planner, so we should not read these as guiding efficient choices on the margin.

Observation on Global games

I was playing around with some visualizations and it seems pretty clear

Move conditional optimality section down

My suggestion is to move this second-best/conditional optimality section until later. It’s present virtue is that several expressions (e.g. \(l_e^*(t_e)\)) are re-used in the private enclosure but I feel it’s present location is a bit of a distraction:

• The primary comparison is between the first-best social and the private enclosure decisions. Why not jump right into that comparison?

• We don’t really do much with the conditional optimal loci right now even though they are some of the more complicated expressions in the paper which complicate/distract right before we’re about to deliver the punchlines of the paper.

• We might draw more interesting discussion moving this discussion later in the paper. The most interesting aspect about it is that it seems to point to a more ‘practical’ policy - govt decides on frontier line but doesn’t try to regulate. For that reason maybe leave it for later when we discuss policy and environment issues (lots of good econ history to tie it too).

Relation \(z\), \(z^*\), \(r\)

From section on conditional optimality we have: $\( z^*(t_e)= \bar l^\alpha \frac{1+(\frac{\Lambda}{\alpha}-1)t_e}{(1+(\Lambda -1)t_e)^{\alpha}} \)$ Let’s try to get this to look a bit more like

\[ \theta F_T(t_e, l_e) \ge c +F_T(t_c,l_c)-\theta F_L(t_e,l_e)\frac{dl_e}{dt_e}+F_L(t_c,l_c)\frac{dl_e}{dt_e} \]

Earlier Appendix notes

All key equations are stated or derived here.

\[\begin{split} T_e+T_c=\bar T \\ L_e+L_c=\bar L \end{split}\]

We define shares of land and labor in the enclosed sector as: \(t_e=\frac{T_e}{\bar T}\) and \(l_e=\frac{L_e}{\bar L}\)

Production technology \(F(T_c, L_c)=T_c^{1-\alpha} \bar L_c ^{\alpha}\) in customary (unenclosed sector). Enclosed sector has potentially different TFP.

\[\begin{split} \begin{align} G(T_{e},L_{e}) &= \theta \cdot t_e^{1-\alpha} \bar l_e ^{\alpha} \cdot \bar T^{1-\alpha} \bar L ^{\alpha}\\ &=F(t_e,l_e)\cdot \theta F(\bar T, \bar L)\\ \end{align} \end{split}\]

Note also for later use that we can write:

\[ APT_e=\frac{F(T_e, L_e)}{T_e}= \bar l ^\alpha \cdot \left ( \frac{l_e}{t_e} \right )^{\alpha} \]

and

\[ MPT_e=(1-\alpha)\cdot \bar l ^\alpha \cdot \left ( \frac{l_e}{t_e} \right )^{\alpha} \]

because for Cobb-Douglas, \(MPT_e=(1-\alpha)\cdot APT_e\)​

Socially Optimal

\[ Y(t_e,l_e)=\left[\theta\cdot F(t_e,l_e)+F(1-t_e,1-l_e)\right ]\cdot F(\bar T, \bar L) \]

Planner wants to maximize social benefits net of enclosure costs

\[ \max_{t_e,l_e} Y(t_e,l_e)-ct_e\bar T \]

We can divide each term above by \(\bar T\) to express in per unit land terms. Then purpose is to maximize:

\[ z(t_e,l_e)-ct_e = \bar l^\alpha [\theta t_e^{1-\alpha}l_e^\alpha +(1-t_e)^{1-\alpha} (1-l_e)^\alpha]-ct_e \]

We break this into tow parts. First find optimal labor-allocation \(l_e^o(t_e)\)​​​​ for any given \(t_e\)​​​​, then search over \(t_e\)​ to find the optimal enclosure rate. This approach makes it easier to compare to equilibria in the decentralized cases. The FOC for optimal labor allocation implies equalization of marginal products across sectors.

\[ \alpha\theta \left ( \frac{t_e}{l_e} \right ) ^{1-\alpha} = \alpha \left ( \frac{1-t_e}{1-l_e} \right ) ^{1-\alpha} \]

Solving for \(l_e\) as a function of \(t_e\):

\[ l_e^o(t_e) = \frac{\Lambda_o t_e}{1+(\Lambda_o-1)t_e}, \quad \text{where }\Lambda_o=\theta^{\frac{1}{1-\alpha}} \]

Substituting this back into \(z(t_e)=z(t_e, l_e^o(t_e))\)​ we have:

\[\begin{split} \begin{aligned} z(t_e) &= \bar l^\alpha \cdot (A + B) \\ &= \theta t_e^{1-\alpha} \left (\frac{\Lambda_o t_e}{1+(\Lambda_o-1)t_e} \right)^\alpha \\ &+ (1-t_e)^{1-\alpha} \left ( 1-\frac{\Lambda_o t_e}{1+(\Lambda_o-1)t_e} \right)^\alpha] \end{aligned} \end{split}\]

To simplify, note that \(A\)​​ can be simplified to

\[ \frac{\theta t_e\cdot \Lambda_0^\alpha}{(1+(\Lambda_o-1)t_e)^\alpha} \]

Now note that \(\theta \cdot \Lambda_0^\alpha=\theta \cdot \theta^\frac{\alpha}{1-\alpha}=\theta^\frac{1}{1-\alpha}=\Lambda_o\) ​​​ so we can further simplify \(A\)​​​ to:

\[ \frac{t_e\cdot \Lambda_0}{(1+(\Lambda_o-1)t_e)^\alpha} \]

Meanwhile \(B\)​ can be written

\[ \frac{1-t_e}{(1+(\Lambda_o-1)t_e)^\alpha} \]

And hence

\[ A+B=\frac{1+(\Lambda_o-1)t_e}{(1+(\Lambda_o-1)t_e)^\alpha}=(1+(\Lambda_o-1)t_e)^{1-\alpha} \]

And \(z(t_e)\) becomes:

\[ z(t_e) = \bar l^\alpha \cdot (1+(\Lambda_o-1)t_e)^{1-\alpha} \]

The marginal benefit of increasing enclosure is then:

\[ z'(t_e)=(1-\alpha)\bar l^\alpha \frac{(\Lambda_o - 1)}{(1+(\Lambda_o-1)t_e)^\alpha} \]

Social Enclosure decisions

When \(\theta \ge 1\)​ (so \(\Lambda^o \geq 1\)​) then \(z(t_e)\)​ is concave in \(t_e\)​ and we can use the derivative of \(z(t_e)\)​ assessed at each endpoint to see whether land enclosure should be zero, partial, or full.

Regime	Condition	Boundary
No Enclosure \(t_e^o=0\)​	z’(0)<0	\(\bar l \le \left[\frac{c}{(1-\alpha)\left(\Lambda^o-1\right)}\right]^{\frac{1}{\alpha}}=l_0^o(c,\theta)\)
Full Enclosure \(t_e^o=1\)​	z’(1)>c	\(\bar l \geq \left[\frac{c \Lambda^o}{(1-\alpha)\left( \Lambda^o-1\right)}\right]^{\frac{1}{\alpha}}=l^o_1(c,\theta)\)
Partial Enclosure	\(z'(t_e)=c\)

Interior social enclosure

Solve \(z'(t_e)=c\) for \(t_e\):

\[ \bar l^\alpha (1-\alpha)(\Lambda_o - 1)=c{(1+(\Lambda_o-1)t_e)^\alpha} \]

\[ \bar l [(1-\alpha)(\Lambda_o - 1)]^{1/\alpha}=c^{1/\alpha}(1+(\Lambda_o-1)t_e) \]

\[ (\Lambda_o-1)t_e= \bar l \left ( \frac{(1-\alpha)(\Lambda_o - 1)}{c} \right )^{1/\alpha}-1 \]

\[ t_e= \frac{\bar l \cdot\left ( {\frac{(1-\alpha)(\Lambda_o-1)}{c}} \right)^{1/\alpha}-1} {(\Lambda_o-1)} \]

\[ t_e= \bar l \cdot (\Lambda_o-1)^\frac{1-\alpha}{\alpha} \cdot \left ( \frac{(1-\alpha)}{c} \right)^{1/\alpha} -\frac{1}{\Lambda_o-1} \]

This could be further simplified perhaps but we’ll leave it at this.

Regime	Condition	Boundary
No Enclosure \(t_e=0\)	z’(0)<0	\(\bar l \le \left[\frac{c}{(1-\alpha)\left(\Lambda^o-1\right)}\right]^{\frac{1}{\alpha}}=l_0^o(c,\theta)\)
Full Enclosure \(t_e=1\)	z’(1)>c	\(\bar l \geq \left[\frac{c \Lambda^o}{(1-\alpha)\left( \Lambda^o-1\right)}\right]^{\frac{1}{\alpha}}=l^o_1(c,\theta)\)
Partial Enclosure	\(z'(t_e)=c\)	n.a.

Interior enclosure

From the condition

\[ \alpha\theta\left(\frac{t_e}{l_e}\right)^{1-\alpha} =\left(\frac{1-t_e}{1-l_e}\right)^{1-\alpha} \]

From which we can solve for

\[ l_e^*(t_e) = \frac{\Lambda t_e}{1+(\Lambda-1) t_e } , \quad \Lambda(\theta)=(\alpha\theta)^\frac{1}{1-\alpha} \]

Private actors enclose when \(r(t_e)>c\)

\[ (1-\alpha)\cdot \theta \cdot \bar l ^\alpha \cdot \left ( \frac{l_e^*(t_e)}{t_e} \right )^{\alpha}>c \]

Substitute in

\[ r(t_e)={\theta}\cdot(1-\alpha)\cdot \bar l^{\alpha} \cdot \left ( \frac{\Lambda}{(1+(\Lambda -1)t_e)} \right)^\alpha >c \]

Interior

\[ {\theta}\cdot(1-\alpha)\cdot \bar l^{\alpha} \cdot \frac{\Lambda^\alpha}{(1+(\Lambda -1)t_e)} =c \]

\[ c(1+(\Lambda -1)t_e)^\alpha={\theta}\cdot(1-\alpha)\cdot \bar l^{\alpha} \cdot {\Lambda^\alpha} \]

\[ c^{1/\alpha}(1+(\Lambda -1)t_e)=[{\theta}\cdot(1-\alpha)]^{1/\alpha}\cdot \bar l \cdot {\Lambda} \]

\[ t_e= \bar l \cdot \frac{\Lambda}{\Lambda-1} \cdot \left [\frac{{\theta}\cdot(1-\alpha)}{c} \right]^{1/\alpha} - \frac{1}{\Lambda-1} \]

When too much or too little enclosure

The question is whether the enclosure rate chosen in a decentralized economy is even ‘second-best’. By this we mean whether, even if we take the labor-misallocation as given, whether net output could be higher at a higher or lower enclosure rate. We can show that it is not even second-best efficient.

To see this note that at any interior private enclosure rate we will have

\[ \theta F(t_e^*, le^*(t_e^*))=c \]

Claim: At \(t_e^*\) we will have \(z'(t_e^*)>c\) meaning that the objective could be raised by raising \(t_e\)

We write out $\( z'(t_e)-c = \theta F_T^e-c -F_T^c + (\theta F_L^e - F_L^c)\cdot \frac{dl_e}{dt_e} \)$

Since the first term \(F_T^e-c\) by assumption the claim is

\[ -F_T^c + (\theta F_L^e - F_L^c)\cdot \frac{dl_e}{dt_e}>0 \]

or that

\[ \boxed{ \begin{aligned} (\theta F_L^e - F_L^c) \cdot \frac{dl_e}{dt_e} > F_T^c \end{aligned} } \]

To prove this note that the labor market condition allows us to substiute for the term in parenthesis, since $\( (\theta F_L - F_L) = F_T \cdot \frac{1-t_e}{1-l_e} \)$

So we can write the benefits> cost case as:

\[ F_T \cdot \frac{1-t_e}{1-l_e} \cdot \frac{dl_e}{dt_e} > F_T \]

or $\( \frac{dl_e}{dt_e} >\frac{1-l_e}{1-t_e} \)$

With the CD we have:

\[ \frac{dl_e}{dt_e} = \frac{\Lambda}{(1+(\Lambda-1)t_e)^2} \]

and

\[ 1-l_e = 1 - \frac{\Lambda t_e}{1+(\Lambda-1)t_e} = \frac{1-t_e}{1+(\Lambda-1)t_e} \]

So \(\frac{1-l_e}{1-t_e} = \frac{1}{1+(\Lambda-1)t_e}\) and we’re left with the inequality being true whenever:

\[ \frac{\Lambda}{(1+(\Lambda-1)t_e)^2}>\frac{1}{1+(\Lambda-1)t_e} \]

hence the inequality comes down to: $\( \frac{\Lambda}{1+(\Lambda-1)t_e}>1 \)$

which can only hold true when \(\Lambda>1\) which is the case when

\(\theta>\theta_H = \frac{1}{\alpha}\) since then \(\alpha \theta>1\) and \(\Lambda>1\)

QED