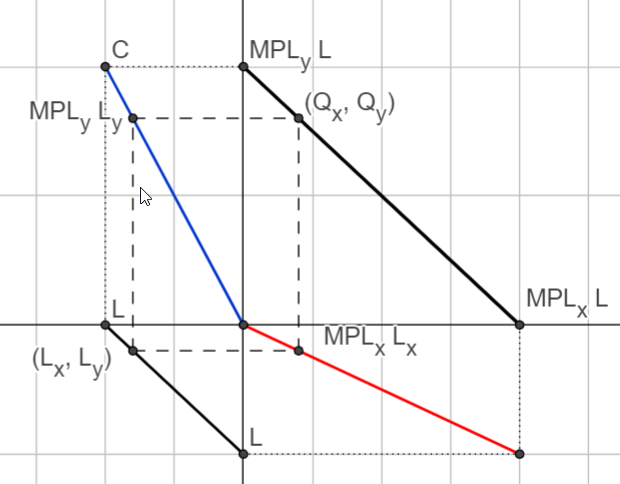
Edgeworth Box

Production allocation efficiency

from hos import *

Efficiency in production

Consider a small-open economy with two production sectors – agriculture and manufacturing – with production in each sector taking place with constant returns to scale production functions. Producers in the agricultural sector maximize profits

\[ \max_{K_A,L_A} p_A F(K_A,L_A) - w L_A - r K_A \]

Producers in manufacturing maximize

\[ \max_{K_M,L_M} p_M F(K_M,L_M) - w L_M - r K_M \]

In equilibrium total factor demands must equal total supplies:

\[ K_A + K_M = \bar K \]

\[ L_A + L_M = \bar L \]

The first order necessary conditions for an interior optimum in each sector lead to an equilibrium where the following condition must hold:

\[ \frac{F_L(K_A,L_A)}{F_K(K_A,L_A)} = \frac{w}{r} =\frac{G_L(\bar K-K_A,\bar L- L_A)}{F_K(\bar K-K_A,\bar L- L_A)} \]

Efficiency requires that the marginal rates of technical substitutions (MRTS) be equalized across sectors (and across firms within a sector which is being assumed here). In an Edgeworth box, isoquants from each sector will be tanget to a common wage-rental ratio line.

If we assume Cobb-Douglas forms \(F(K,L) = K^\alpha L^{1-\alpha}\) and \(G(K,L) = K^\beta L^{1-\beta}\) the efficiency condition can be used to find a closed form solution for \(K_A\) in terms of \(L_A\):

\[\frac{(1-\alpha)}{\alpha}\frac{K_A}{L_A} =\frac{w}{r} =\frac{(1-\beta)}{\beta}\frac{\bar K-K_A}{\bar L-L_A}\]

Rearranging the expression above we can get a closed-form expression for the efficiency locus \(K_A (L_A)\):

\[ K_A(L_A) = \frac{L_A \cdot \bar K} { \frac{\beta(1-\alpha)}{\alpha (1-\beta)} (\bar L -L_A)+L_A} \]

With this we can now plot the efficiency locus curve in an Edgeworth box.

Edgeworth Box plots

Here is and Edgeworth Box depicting the situation where \(L_A = 50\) units of labor are allocated to the agricultural sector and all other allocations are efficient (along the efficiency locus).

edgeplot(50)

(LA,KA)=(50.0, 69.2)  (QA, QM)=(60.8, 41.2)  RTS= 2.1

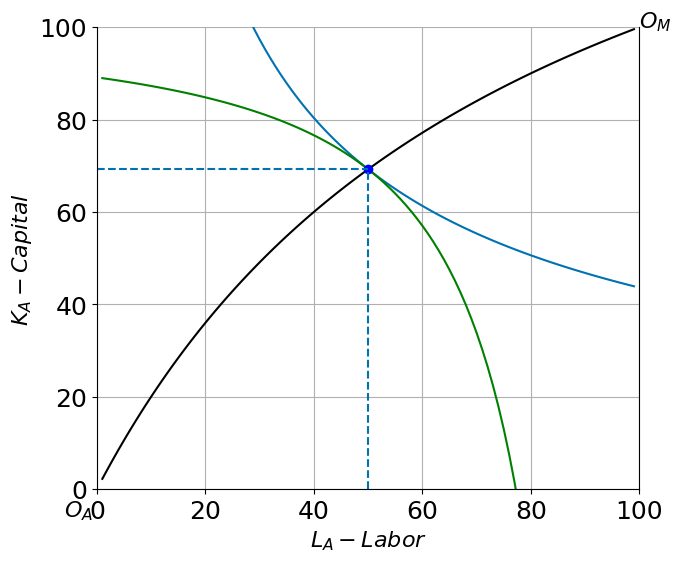
If you’re reading this using a jupyter server you can interact with the following plot, changing the technology parameters and position of the isoquant. If you are not this may appear blank or static.

LA = 50
interact(edgeplot, LA=(10, Lbar-10,1), 
         Kbar=fixed(Kbar), Lbar=fixed(Lbar),
         alpha=(0.1,0.9,0.1),beta=(0.1,0.9,0.1));

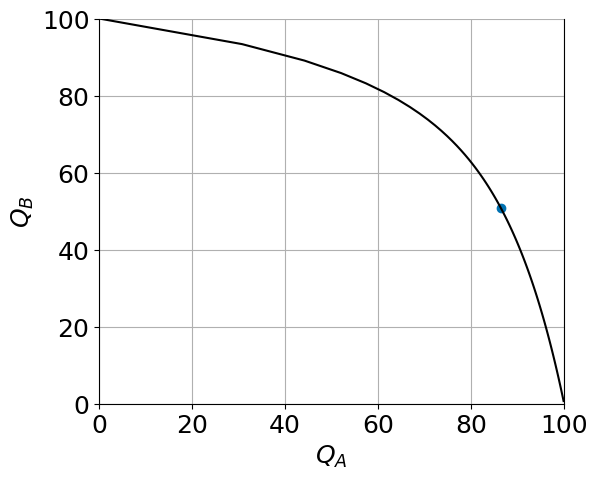
The Production Possiblity Frontier

The efficiency locus also allows us to trace out the production possibility frontier: by varying \(L_A\) from 0 to \(\bar L\) and, for every \(L_A\), calculating \(K_A(L_A)\) and with that efficient production \((q_A,q_B)\) where \(q_A=F(K_A(L_A), L_A)\) and \(q_B=F(\bar K - K_A(L_A), \bar L - L_A)\).

For Cobb-Douglas technologies the PPF will be quite straight unless \(\beta\) and \(\alpha\) are very different from each other! (In practical terms what this means is that quite small changes to product prices will move around production quite a bit)

ppf(30,alpha =0.9, beta=0.1)

Jump to the notebook on the Hecksher-Ohlin-Samuelson to see a very practical application of the Edgeworth Box and this basic model framework and derive a number of theorems regarding how a small open econonomy will respond to a change in world relative prices or factor endowments.