Heckscher-Ohlin-Samuelson - Teaching Economics

Model of Trade¶

See the Edgeworth Box notebook to understand how the Edgeworth Box diagrams drawn below were constructed to represent this economy.

from hos import *

Model Parameters¶

This notebook explores the HOS model with:

$\alpha$ = 0.6: Capital share in agriculture (default)
$\beta$ = 0.4: Capital share in manufacturing (default)
$\bar{K}$ = 100: Total capital endowment
$\bar{L}$ = 100: Total labor endowment

We’ll explore how equilibrium changes with different world prices and factor endowments.

Consider a small-open economy with two production sectors -- agriculture and manufacturing -- with production in each sector taking place with constant returns to scale production functions. Producers in the agricultural sector maximize profits

\max_{K_A,L_A} P_A F(K_A,L_A) - w L_A - r K_A

(1)

Producers in manufacturing maximize

\max_{K_M,L_M} P_M G(K_M,L_M) - w L_M - r K_M

(2)

In equilibrium total factor demands must equal total supplies:

K_A + K_M = \bar K

(3)

L_A + L_M = \bar L

(4)

Here is an Edgeworth Box that depicts the situation where $L_A = 50$ units of labor are allocated to the agricultural sector and all other allocations are efficient (along the efficiency locus).

Here is an [Edgeworth Box](Edgeworth.ipynb_ that depicts the situation where $L_A = 50$ units of labor are allocated to the agricultural sector and all other allocations are efficient (along the efficiency locus).

edgeplot(50)

(LA, KA) = (50.0, 69.2)  (QA, QM) = (60.8, 41.2)  RTS =  2.1

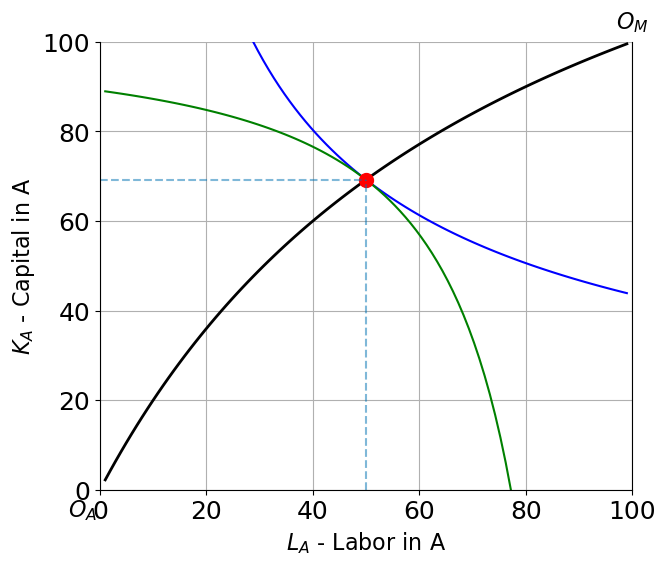
If you’re reading this using a jupyter server you can interact with the following plot, changing the technology parameters and position of the isoquant. If you are not this may appear blank or static.

LA = 50
interact(edgeplot, LA=(10, Lbar-10,1), 
         Kbar=fixed(Kbar), Lbar=fixed(Lbar),
         alpha=(0.1,0.9,0.1),beta=(0.1,0.9,0.1));

Loading...

Resource Allocation in a small open economy¶

From the first order conditions for profit maximization in each sector we have:

P_A F_L(K_A,L_A) = w = P_M G_L(K_M,L_M)

(5)

The Stolper-Samuelson Line¶

We can derive a relationship between relative product prices (set on the world market) and the equilibrium wage-rental ratio $w/r$ .

With the Cobb-Douglas technology we can write:

F_L = (1-\alpha) \left [ \frac{K_A}{L_A} \right]^\alpha

(6)

F_K = \alpha \left [ \frac{K_A}{L_A} \right]^{\alpha-1}

(7)

The first order necessary conditions for an interior optimum in each sector lead to an equilibrium where the following condition must hold:

\frac{F_L(K_A,L_A)}{F_K(K_A,L_A)} = \frac{w}{r} =\frac{G_L(\bar K-K_A,\bar L- L_A)}{G_K(\bar K-K_A,\bar L- L_A)}

(8)

With the Cobb Douglas technology we can write:

F_L = (1-\alpha) \left [ \frac{K_A}{L_A} \right]^\alpha

(9)

F_K = \alpha \left [ \frac{L_M}{K_M} \right]^\alpha

(10)

The first order necessary conditions for an interior optimum in each sector lead to an equilibrium where the following condition must hold:

\frac{F_L(K_A,L_A)}{F_K(K_A,L_A)} = \frac{w}{r} =\frac{G_L(\bar K-K_A,\bar L- L_A)}{G_K(\bar K-K_A,\bar L- L_A)}

(11)

Using these expressions and earlier factor demand expressions we can derive:

\frac{P_A}{P_M} =\frac{1-\alpha}{1-\beta} \frac{\left [ \frac{ (1-\beta)}{\beta} \frac{w}{r} \right]^\beta} { \left [ \frac{ (1-\alpha)}{\alpha} \frac{w}{r} \right]^\alpha}

(12)

or

\frac{P_A}{P_M} = \Gamma \left [ \frac{w}{r} \right]^{\beta - \alpha}

(13)

where

\Gamma = \frac{1-\alpha}{1-\beta} \left ( \frac{\alpha}{1-\alpha} \right )^\alpha \left ( \frac{1-\beta}{\beta} \right )^\beta

(14)

Inverting, we get an expression for the Stolper Samuelson Line

The Stolper-Samuelson Theorem¶

The Stolper-Samuelson theorem tells us how changes in the world relative price of products translates into changes in the relative price of factors and therefore in the distribution of income in society.

The theorem states that an increase in the relative price of a good will lead to an increase in both the relative and the real price of the factor used intensively in the production of that good (and conversely to a decline in both the real and the relative price of the other factor).

The Stolper Samuelson Theorem¶

The Stolper Samuelson theorem tells us how changes in the world relative price of products translates into changes in the relative price of factors and therefore in the distribution of income in society.

The theorem states that an increase in the relative price of a good will lead to an increase in both the relative and the real price of the factor used intensively in the production of that good (and conversely to a decline in both the real and the relative price of the other factor).

This relationship can be seen from the formula. If agriculture were more labor intensive than manufacturing, so $\alpha < \beta$ , then an increase in the relative price of agricultural goods creates an incipient excess demand for labor and an excess supply of capital (as firms try to expand production in the now more profitable labor-intensive agricultural sector and cut back production in the now relatively less profitable and capital-intensive manufacturing sector). Equilibrium will only be restored if the equilibrium wage-rental ratio falls which in turn leads firms in both sectors to adopt more capital-intensive techniques. With more capital per worker in each sector output per worker and hence real wages per worker $\frac{w}{P_a}$ and $\frac{w}{P_m}$ increase.

Solving for Equilibrium Allocation¶

Solving for equilibrium allocation as a function of relative price p¶

Code to solve for unique HOS equilibrium as a function of world relative price $\frac{P_A}{P_M}$

From Lerner-Edgeworth box

Equilibrium in the capital market:

K_A + K_M = \bar K

(15)

We can use $K_A= k_A \cdot L_A$ and $K_M = k_M \cdot L_M$ to rewrite this as:

k_A\cdot L_A + k_M \cdot L_M = \bar K

(16)

Noting that $L_M=\bar L - L_A$ and solving for $L_A$ :

k_A\cdot L_A = \bar K - k_M \cdot (\bar L -L_A)

(17)

L_A = \frac{\bar K - k_M \cdot \bar L}{k_A-k_M}

(18)

We now have enough to solve the model. If the economy is open to trade, it takes world prices as given. For example if $\frac{P_A}{P_M}=1$ then we can find $w/r$ and from that optimal capital intensities in each industry $k_A$ and $k_M$ .

from IPython.display import display, Markdown
p = 1
a = 0.3
b = 0.7
wr = wreq(p, a=a, b=b)
ka = kl(wr,a)
km = kl(wr,b)
LA, KA = hos_eq(p, Kbar=100, Lbar=100)

display(Markdown(rf"""
  When $\frac{{P_a}}{{P_m}}=1, \frac{{w}}{{r}}$ = {wr:0.2f} 
  and $(k_a, k_m)$ = ({ka:0.2f}, {km:0.2f}) 
  """))

Loading...

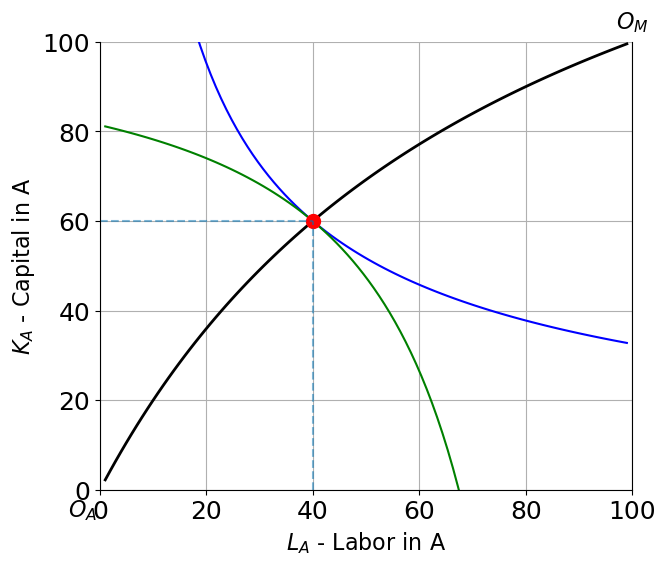
Lerner Diagram¶

The Lerner diagram shows factor market equilibrium with isoquants and factor intensity rays.

HOS(1)

(LA, KA) = (40.0, 60.0)  (QA, QM) = (51.0, 51.0)  RTS =  2.2

HOS(1.06)

(LA, KA) = ( 9.7, 19.4)  (QA, QM) = (14.7, 86.3)  RTS =  3.0

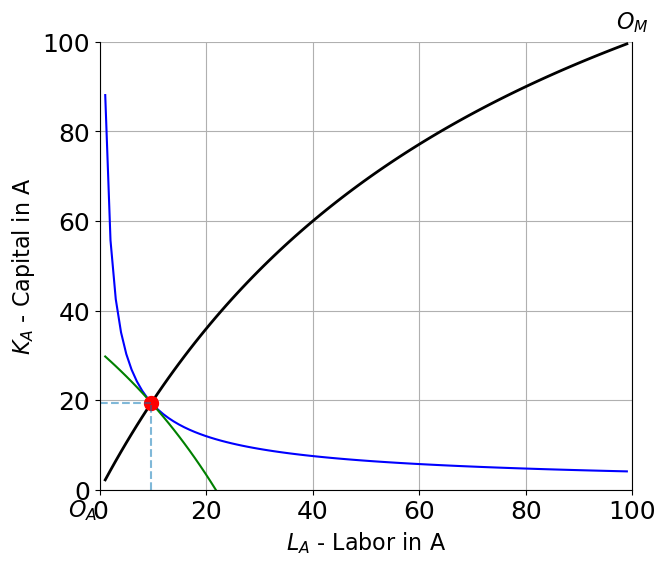
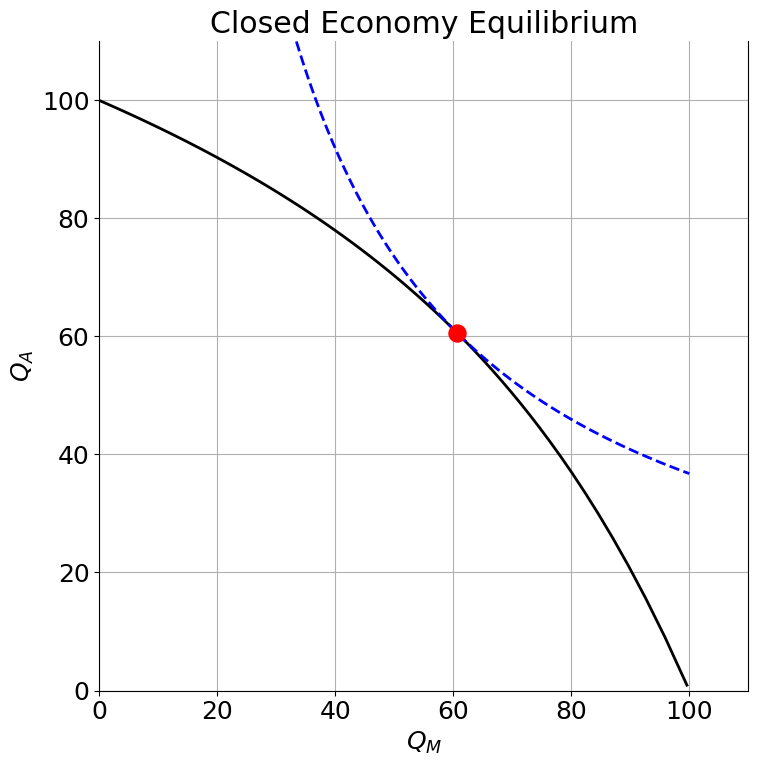
Closed Economy (Autarky)¶

In a closed economy without trade, production must equal consumption. The economy produces where the PPF is tangent to the highest indifference curve.

The Rybczynski Theorem¶

The Rybczynski theorem shows how changes in factor endowments affect production. An increase in a factor endowment will lead to a more than proportional increase in output of the good that uses that factor intensively, and a decrease in output of the other good (at constant prices).

klplot(1)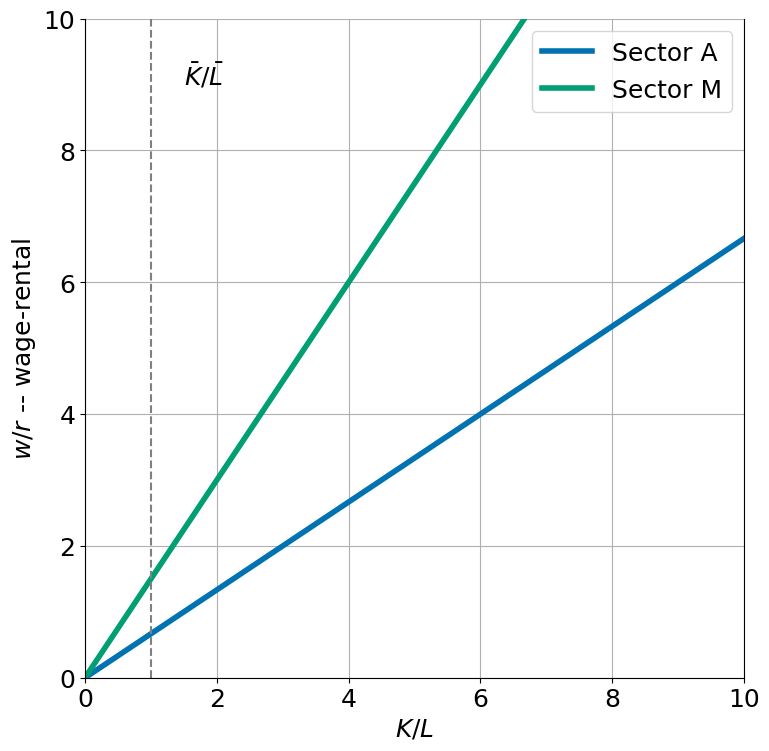

# Rybczynski Theorem: Effect of labor endowment increase
print("Rybczynski Theorem Demonstration")
print("(Manufacturing is labor-intensive: β=0.35 > α=0.65)\n")

print("Initial endowment (Kbar=100, Lbar=100):")
eq1 = calculate_hos_equilibrium(1, Kbar=100, Lbar=100, alpha=0.65, beta=0.35)
print(f"  QA = {eq1['QA']:.1f}, QM = {eq1['QM']:.1f}")
print(f"  LA = {eq1['LA']:.1f}, LM = {eq1['LM']:.1f}")

print("\nAfter 50% labor increase (Kbar=100, Lbar=150):")
eq2 = calculate_hos_equilibrium(1, Kbar=100, Lbar=150, alpha=0.65, beta=0.35)
print(f"  QA = {eq2['QA']:.1f}, QM = {eq2['QM']:.1f}")
print(f"  LA = {eq2['LA']:.1f}, LM = {eq2['LM']:.1f}")

print(f"\nChanges: ΔQA = {eq2['QA']-eq1['QA']:.1f}, ΔQM = {eq2['QM']-eq1['QM']:.1f}")
print("Labor-intensive manufacturing expands, capital-intensive agriculture contracts!")

Rybczynski Theorem Demonstration
(Manufacturing is labor-intensive: β=0.35 > α=0.65)

Initial endowment (Kbar=100, Lbar=100):
  QA = 52.3, QM = 52.3
  LA = 35.0, LM = 65.0

After 50% labor increase (Kbar=100, Lbar=150):
  QA = 21.8, QM = 109.0
  LA = 14.6, LM = 135.4

Changes: ΔQA = -30.5, ΔQM = 56.7
Labor-intensive manufacturing expands, capital-intensive agriculture contracts!

Rybczynski Theorem Demonstration¶

Adding labor should more than proportionately expand the production of the labor-intensive product and reduce the production of the other good.

Here manufacturing is the labor-intensive sector (β > α). We increase $\bar{L}$ from 100 to 150 and we see how in the new equilibrium labor in manufacturing goes up from $L_M=65$ to $L_M=135$ . Output of manufacturing increases from 51 to 106 and output of agriculture falls from 51 to 21.

interact(lerner, p=(0.7,1.4,0.1));

Loading...

closed_plot(alpha=0.8, beta=0.2)

Autarky: (QA, QM) = (60.6, 60.6)

C:\Users\jonat\My Drive\code\GitHub\EconTeach\notebooks\trade\hos.py:82: RuntimeWarning: invalid value encountered in scalar power
  return K**alpha * L**(1-alpha)

interact(closed_plot, alpha=(0.1,0.9,0.1), beta=(0.1,0.9,0.1));

Loading...

NOTE: Something is off on this Rybyczynski Edgeworth plot... had been working..

rybplot(1, Kbar=Kbar, Lbar=Lbar, alpha=0.65, beta=0.35)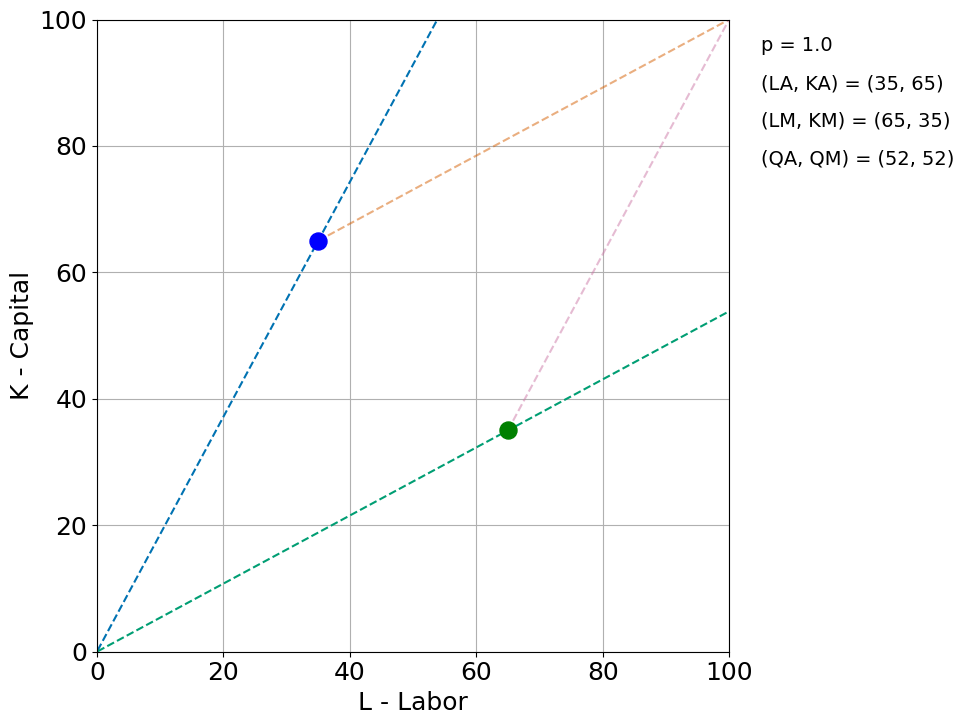

Rbyczynski Theorem. Adding labor should more than proportionately expand the productinon of the labor-intensive product and reduce the production of the other good. Here Manufacturing is the labor-intensive sector. We added increase $\bar L$ from 100 to 150 and we see how in the new equilibrium labor in manufacturing goes up from $L_M=65$ to $L_M=135$ . Output of manufacturing increases from 51 to 106 and output of agriculture falls from 51 to 21.

rybplot(1, Kbar=Kbar, Lbar=Lbar*1.5, alpha=0.65, beta=0.35)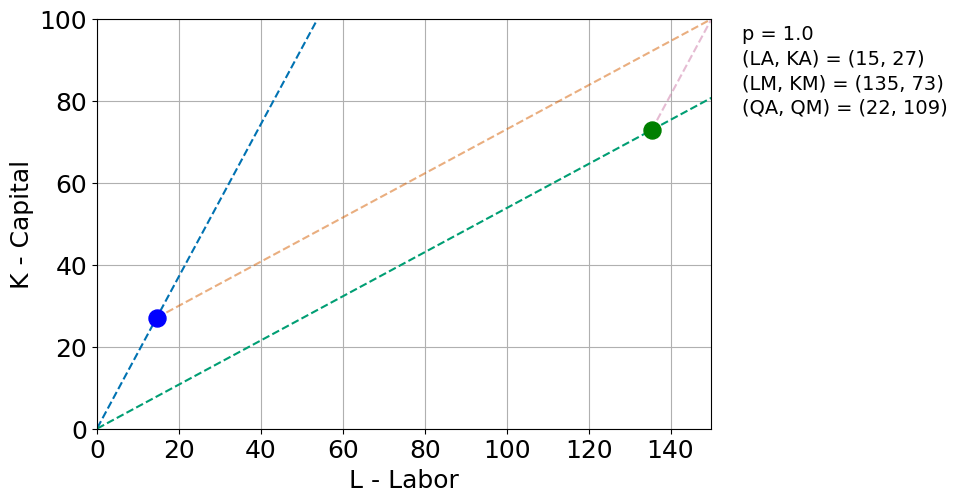

interact(rybplot, p = fixed(1), Lbar =(50,150,10), Kbar =(50,150,10), alpha=fixed(0.65), beta=fixed(0.35));

Loading...